Parallel Resistor Calculator

Understanding Resistors in Parallel

When resistors are connected in parallel, the total or equivalent resistance of the circuit decreases. This decrease happens because the electric current has multiple paths to follow, thus reducing the overall resistance faced. Each resistor in parallel has the same voltage across it but can carry different currents depending on its resistance.

How to Calculate

The formula to find the total resistance R_total of resistors in parallel is given by the reciprocal of the sum of the reciprocals of each individual resistor's resistance:

where:

R₁, R₂, R₃, . . . ,R_n are the resistances of each resistor in the parallel circuit.

Example

Suppose you have three resistors in parallel with resistances of 100 ohms, 200 ohms, and 300 ohms. To find the total resistance, use the formula:

Calculating this, we find:

So, when we calculate the total resistance R_total is:

Visual Representation

Visualizing this in a circuit:

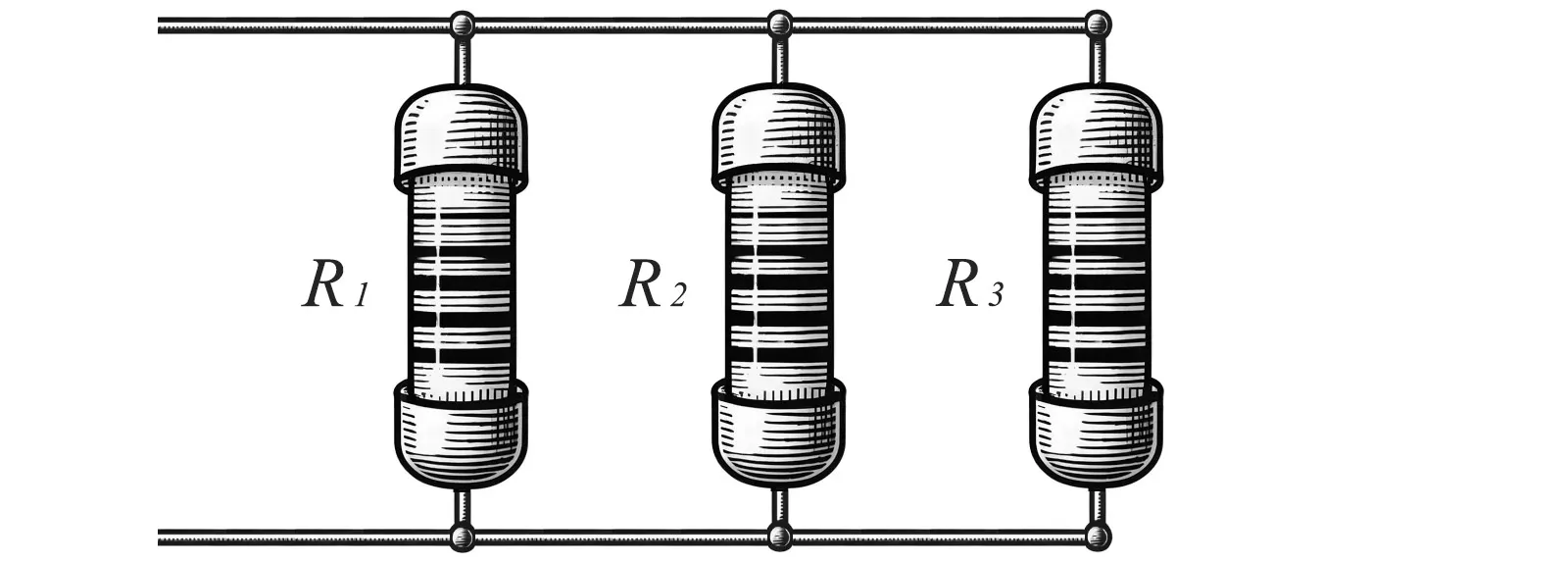
Imagine each resistor connected at both ends to the same two points in the circuit, forming a parallel pathway for the current. This parallel connection allows the current to be split among the resistors according to their individual resistances.

Key Points

• Total Resistance Decreases: In parallel, the total resistance is always less than the smallest resistance of any resistor in the parallel group.
• Voltage is Constant: The voltage across each resistor in a parallel circuit is the same, though the current through each can vary.

This calculation method is crucial for designing electronic circuits where a lower resistance is needed than any of the individual resistors available, or where the power distribution across components is a concern. It also highlights the practical aspect of resistors in managing current flow in various circuit configurations.